Everyday Algorithms: Sorting clothes fast

A few months ago I started Austria’s compulsory community service at an institution for mentally handicapped people, where I assisted professionally educated carers with some tasks there. A pretty common task there was to put recently washed clothes in people’s closets. (the people we cared for were accommodated in the institution’s residential home). Each Tuesday and Thursday we got about 12 boxes including the washed clothes (the count varied from 5 to 30 pieces, let’s say the average count was 20 ). Compared with other tasks I had to do, putting clothes in the closets was a relaxing activity, but sometimes it got boring and I just wanted to finish it as fast as I could.

So, I wondered how I could optimize the task of putting clothes in a closet and therefore reduce the time and effort it takes.
If you look at the following graphic, you can see the defining conditions of my problem:

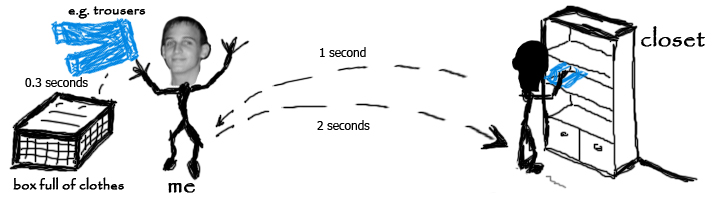
I have one box full of unsorted clothes for each room. The clothes in each box have to be put in one room’s closet. The trajectory from the box of clothes to the closet takes about 2 seconds, the way from the closet to the box takes 1 second (the time of the return differs from the initial way because the actual placing of clothes was taken into account). Let’s assume that taking a piece of clothing takes 0.3 seconds.

And here’s the magic formula for my optimization approach:
Group clothes.

By grouping clothing it’s possible to minimize the distance which has to be walked from the box to the closet. Let’s think of a really slow technique for putting clothes in a closet. E.g. think of the situation where you take each piece of clothing out of the box, go to the closet, put it in and return to the box. That would’ve resulted in the maximum amount of time that could be consumed (assuming you didn’t fall asleep and performed the actions and tasks in the time alloted to them). If you grouped clothes into heaps you would only have to walk the distance for each heap, which is in the most cases less than the count of clothes. It’s just as simple as it sounds but the amount of time and effort reduction really pays off.

For a better understanding, here are two examples with the numbers from above filled in. The first one implements the slow algorithm, the second one uses the fast algorithm.

Example using the slow algorithm

Patrick decided to take each piece of clothing and put it in the closet. The box contains (as mentioned above) 20 pieces of clothing. He takes the first piece of clothing (0.3 seconds) walks to the closet, places the piece in it (2 seconds) and returns to the box (1 second). He takes the second piece …
20 * ( 0.3 + 2 + 1 ) = 20 * 3.3 = 66 seconds.

Example using the fast algorithm

Pa7 decided to group the clothes first and then put them as heaps in the closet. The box contains 20 pieces of clothing, they can be classified as one of 6 clothing groups (socks, underwear, wests, pullovers, trousers, shirts). He takes the first piece of clothing (0.3 seconds). It’s a west. There isn’t a heap for wests here yet -> he creates one. He takes the second piece (0.3 seconds). It’s a west again. He puts it on the wests heap. He takes the third piece. It’s a sock. -> He creates a new heap. , …
20 * 0.3 + 5 * (2 + 1) = 6.6 + 15 = 21.6 seconds.

Saved more than 50% of time. But the time/effort reduction strongly depends on how many groups you have. If you have only one group and you know that you only have one group (you don’t have to take each piece out of the box and put it on a heap) the time consumption reaches a minimum.

Summing up. Here is the pseudo code for my algorithm:

for each piece of clothing
check whether there is already an existing group for it
if there is a group: add it to the group
otherwise create a new clothing-group

for each clothing-group
put the group of clothing into the chest

Drawbacks

As I pointed out in the section above, in most cases the clothes heap count is less than the clothes count. If that’s not true, the grouping algorithm takes as long as the slow algorithm since you’d have to create a new clothes group(heap) for each piece of clothing and walk the distance clothes count times. But that basically means that in any case where there are less heaps than clothes, the algorithm pays off. In reality the algorithm also wouldn’t be fast when the heap count is huge since a single group action would take more time, but I can’t imagine that anyone would ever group/classify his/her clothes in more than 10 clothes-classes, otherwise (s)he missed the point of generalization/abstraction :)

You may implement the algorithm with your own body’s programming language ;-)

Feedback is very welcome. Do you know a better technique or have your own algorithms for everyday challenges? Let me know your thoughts about it, make a comment or ping me on twitter @patrickwied